FUNÇÕES COMPLEXAS
Mário, um ciclista acrobático, vai atravessar de um prédio a outro com uma super bicicleta , percorrendo a distância sobre um cabo de aço, como demonstra o esquema a seguir:
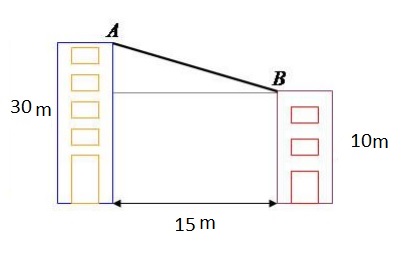
Qual é a distância que Mário irá percorrer pelo cabo de aço?
22 m
25 m
18 m
30 m
15 m
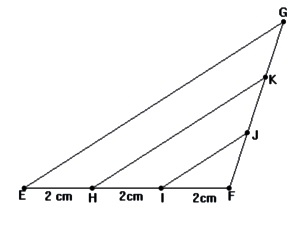
A fachada de um antigo casarão contém triângulos semelhantes, como os triângulos desta figura:

A razão entre os perímetros dos triângulos maior e menor vale :





Convertendo os ângulos 1080° em radianos e 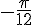 para graus.
para graus.
- 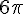 e 15°
e 15°
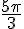 e -18°
e -18°
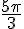 e 18°
e 18°
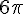 e - 15°
e - 15°
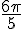 e -15°
e -15°
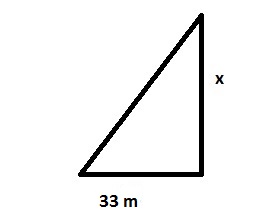
Em uma subida de índice igual a 1/3 se afastarmos 33 m, a quantos metros nos elevaremos do chão?
11 m
5,5 m
18 m
44 m
13 m
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
5,52 metros
15,6 metros
22,56 metros
10,56 metros
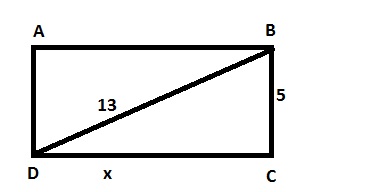
O número complexo pode ser escrito na sua forma algébrica, a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo assim o módulo de O módulo de é exatamente igual a:
-2
-1
3
2
1
Associe as duas colunas, relacionando o sinal da função seno aos seus respectivos quadrantes:
Sen > 0
( ) 1º quadrante
2. Sen < 0
( ) 2ª quadrante
( ) 3ª quadrante
( ) 4ª quadrante
A sequência correta dessa associação é
(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
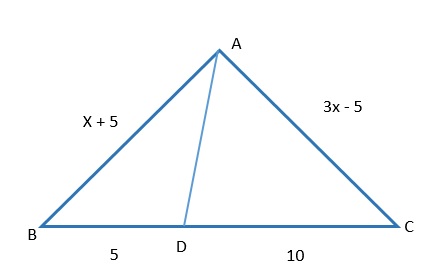
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.

22 m
25 m
18 m
30 m
15 m
A fachada de um antigo casarão contém triângulos semelhantes, como os triângulos desta figura:

A razão entre os perímetros dos triângulos maior e menor vale :





Convertendo os ângulos 1080° em radianos e 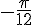 para graus.
para graus.
- 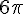 e 15°
e 15°
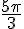 e -18°
e -18°
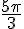 e 18°
e 18°
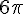 e - 15°
e - 15°
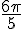 e -15°
e -15°
Em uma subida de índice igual a 1/3 se afastarmos 33 m, a quantos metros nos elevaremos do chão?

11 m
5,5 m
18 m
44 m
13 m
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
5,52 metros
15,6 metros
22,56 metros
10,56 metros
O número complexo pode ser escrito na sua forma algébrica, a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo assim o módulo de O módulo de é exatamente igual a:
-2
-1
3
2
1
Associe as duas colunas, relacionando o sinal da função seno aos seus respectivos quadrantes:
Sen > 0
( ) 1º quadrante
2. Sen < 0
( ) 2ª quadrante
( ) 3ª quadrante
( ) 4ª quadrante
A sequência correta dessa associação é
(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.

Convertendo os ângulos 1080° em radianos e 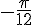 para graus.
para graus.
- 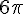 e 15°
e 15°
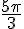 e -18°
e -18°
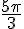 e 18°
e 18°
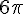 e - 15°
e - 15°
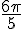 e -15°
e -15°
Em uma subida de índice igual a 1/3 se afastarmos 33 m, a quantos metros nos elevaremos do chão?

11 m
5,5 m
18 m
44 m
13 m
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
5,52 metros
15,6 metros
22,56 metros
10,56 metros
O número complexo pode ser escrito na sua forma algébrica, a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo assim o módulo de O módulo de é exatamente igual a:
-2
-1
3
2
1
Associe as duas colunas, relacionando o sinal da função seno aos seus respectivos quadrantes:
Sen > 0
( ) 1º quadrante
2. Sen < 0
( ) 2ª quadrante
( ) 3ª quadrante
( ) 4ª quadrante
A sequência correta dessa associação é
(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.

-
Em uma subida de índice igual a 1/3 se afastarmos 33 m, a quantos metros nos elevaremos do chão?

11 m
5,5 m
18 m
44 m
13 m
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
5,52 metros
15,6 metros
22,56 metros
10,56 metros
O número complexo pode ser escrito na sua forma algébrica, a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo assim o módulo de O módulo de é exatamente igual a:
-2
-1
3
2
1
Associe as duas colunas, relacionando o sinal da função seno aos seus respectivos quadrantes:
Sen > 0
( ) 1º quadrante
2. Sen < 0
( ) 2ª quadrante
( ) 3ª quadrante
( ) 4ª quadrante
A sequência correta dessa associação é
(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.


11 m
5,5 m
18 m
44 m
13 m
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
5,52 metros
15,6 metros
22,56 metros
10,56 metros
O número complexo pode ser escrito na sua forma algébrica, a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo assim o módulo de O módulo de é exatamente igual a:
-2
-1
3
2
1
Associe as duas colunas, relacionando o sinal da função seno aos seus respectivos quadrantes:
Sen > 0
( ) 1º quadrante
2. Sen < 0
( ) 2ª quadrante
( ) 3ª quadrante
( ) 4ª quadrante
A sequência correta dessa associação é
(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.

7,36 metros
5,52 metros
15,6 metros
22,56 metros
10,56 metros
O número complexo pode ser escrito na sua forma algébrica, a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo assim o módulo de O módulo de é exatamente igual a:
-2
-1
3
2
1
Associe as duas colunas, relacionando o sinal da função seno aos seus respectivos quadrantes:
Sen > 0
( ) 1º quadrante
2. Sen < 0
( ) 2ª quadrante
( ) 3ª quadrante
( ) 4ª quadrante
A sequência correta dessa associação é
(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.

-2
-1
3
2
1
Associe as duas colunas, relacionando o sinal da função seno aos seus respectivos quadrantes:
Sen > 0
( ) 1º quadrante
2. Sen < 0
( ) 2ª quadrante
( ) 3ª quadrante
( ) 4ª quadrante
A sequência correta dessa associação é
(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.

(2),(2),(1),(1)
(1),(2),(1),(2)
(2),(1),(2),(1)
(2),(1),(2),(2)
(1),(1),(2),(2)
No triângulo ABC,  é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.

 é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.
é bissetriz interna, AB = x + 5 cm, AC =3x -5 cm e BC = 15 cm. Encontre o valor do segmento AC.